কোয়ান্টাম মেকানিক্স ০৮: পরিসংখ্যানিক মেকানিক্স এবং কোয়ান্টাম স্ট্যাটিস্টিক্

 

শিবু একদিন স্বপ্নে চলে গেল ‘কণার শহর’-এ। সেখানে ছোট ছোট গ্যাসকণা সবাই বসে আছে এক বিশাল শপিং মলে। হঠাৎ সমাজপতি মিঃ ম্যাক্সওয়েল–বলৎসম্যান(!) এসে ঘোষণা করলেন,“প্রতি মুহূর্তে তোমরা যেভাবে দেয়ালের সাথে ধাক্কা দেবে, সেটাই গ্যাসের ‘চাপ’। বেশি ধাক্কা মানে বেশি চাপ!”কণাগুলো উৎসাহে দেয়ালে লাফিয়ে উঠল, আর শিবু দেখতে পেল দেয়াল থেকে ‘ধাক্কা’ আসলে কণার গতি ও সংখ্যালঘু নাশকতার মুদ্রায় পরিণত হচ্ছে।

তখন হাজির হলেন ম্যাডাম পার্টিশন ফাংশন নামে এক কবিতার ডাক্তার। তিনি বললেন,“আমি তোমাদের প্রতিটি মাইক্রো–অবস্থা গুনে গুনে রাখি, তার নাম আমার পার্টিশন ফাংশন $Z$। আমার হিসাবেই বের হয় ক’টা কণা কী গভীরে দোলা দেবে, কতটা এনার্জি থাকবে, আর পরোক্ষভাবে চাপ আর তাপমাত্রা।”শিবু অবাক হয়ে দেখতে পেল, প্রতিটি কণার ছোট–বড় গতি $e^{-E_i\mathrm{/}(k_{B}T)}$অনুপাতে প্রসারিত হচ্ছে, যেন প্রত্যেকেই তার ‘পাওয়ার লেভেল’ অনুযায়ী নাচছে।

এরপর এল ফার্মি ভাই আর বোসি মামা। ফার্মি ভাই একদম অদ্ভুত—“আমার বাসে একবারে একটিতেই আসবে, কারণ Pauli exclusion-এর নিয়ম,”—বললেন তিনি, আর শিবু বুঝল, ফার্মিয়নরা এক কোয়ান্টাম সিট ভাগাভাগি করতে পারে না।বোসি মামা হাসি দিয়ে বললেন, “আমার বাসে যত ইচ্ছে কইরা মজা করো! কারণ Bose–Einstein বণ্টনে একাধিক বস এক সিটে হা–হা করে বসে থাকতে পারে।”

শিবু দেখল, বসেরা একসাথে জমে জমে ‘কোল্ড পার্টি’ করতে পারে—বোজ-আইনস্টাইন সংঘন নামক এক অদ্ভুত অনুষ্ঠান!

শেষে সবাই মিলে শিবুকে পাঠালো ‘গ্র্যান্ড এন্সেম্বল থিয়েটারে’—সেখানে রাসায়নিক সম্ভাব্যতা μযুক্ত হলে বসে বসে গড়ে কতজন আসবেন আর চলে যাবেন, সেই হিসাব চলে। শিবু বুঝল,– গ্যাসের ক্লাসিক্যাল খেলায় কণা যতই ভাসবে, তার সব মাইক্রোস্টেট সমান গুরুত্বের দৌড়ে অংশ নেয় (Equal a priori probability),– আর কোয়ান্টাম রাজ্যে ফার্মিয়ন-ফের্মিয়ন আর বস–বসের আলাদা–আলাদা টিকিট আছে (Fermi–Dirac vs Bose–Einstein)।

সকালে ঘুম থেকে জেগে শিবু স্বপ্নের গল্প মনে করল। আর বুঝল—ব্যাচেলর লাইফের মত গ্যাসে যত বিশৃঙ্খলা, তাতে লুকিয়ে আছে চাপ, তাপ, এনার্জি—সবই পরিসংখ্যানিক মেকানিক্স আর কোয়ান্টাম স্ট্যাটিস্টিক্সের মাস্টারপ্ল্যান!

১. পরিসংখ্যানিক মেকানিক্স (Statistical Mechanics)

পরিসংখ্যানিক মেকানিক্স হলো বহুসংখ্যক অণু বা কণার গড় ব্যবহারিক আচরণ থেকে তাপগতীয় এবং মেকানিক্যাল বৈশিষ্ট্য বিবেচনা করার শাস্ত্র। একটি সিস্টেমে প্রতিটি কণার সঠিক গতিবিদ্যা অজানা থাকলেও, সেগুলোর গড়—যেমন তাপমাত্রা, চাপ, এনার্জি বিতরণ—সূত্র দ্বারা খুঁজে বের করা যায়।

শুরু করার উদাহরণ:

• ধরা যাক একটি বাক্সে হাজার হাজার গ্যাস মলিকুলের সমষ্টি আছে।

• আমরা একেকটি কণার গতিবিদ্যা (গতি, অবস্থান) স্পষ্টভাবে ট্র্যাক করি না, বরং তাদের গড় গতিবেগের উপর ভিত্তি করে তাপমাত্রা নির্ধারণ করি।

• পরিসংখ্যানিক মেকানিক্স বলবে, “এই তাপমাত্রায় কণাগুলোর গতিবেগের বণ্টন হবে Maxwell–Boltzmann বণ্টন,” অর্থাৎ অধিকাংশ কণার গতি গড়ের কাছাকাছি থাকবে, কিছু কণা দ্রুত এবং কিছু ধীর হবে।

• এর ভিত্তিতে আমরা সহজেই হিসাব করতে পারি—বাক্সের চাপ কত হবে, এনার্জি কত স্থায়ী হবে, ইত্যাদি।

২. কোয়ান্টাম স্ট্যাটিস্টিক্স (Quantum Statistics)

কোয়ান্টাম স্ট্যাটিস্টিক্স হলো পরিসংখ্যানিক মেকানিক্সের একটি বিস্তৃত রূপ, যেখানে কণাগুলোকে তাঁর কোয়ান্টাম প্রকৃতির (ইন্ডিস্টিংগুইশেবল বা অপরিচ্ছেদ্যতা) উপর ভিত্তি করে সাম্যবণ্টিত (distribution) ভাবে বিবেচনা করা হয়। এখানে দুই ধরনের প্রধান বণ্টন আছে:

• Fermi–Dirac Statistics (ফের্মিয়নদের জন্য)

• Bose–Einstein Statistics (বসদের জন্য)

শুরু করার উদাহরণ:

• ফের্মিয়ন (Fermion): যেমন ইলেকট্রন, যা দুইটি বা তার কম ইলেকট্রন একই কোয়ান্টাম অবস্থা (energy level, spin, ইত্যাদি) সামলাতে পারে না (Pauli exclusion principe)।

  • উদাহরণ: ধরা যাক ধাতুর একটি পাতায়ে অনেক ইলেকট্রন আছে; Fermi–Dirac বণ্টন বলে, “ঠান্ডা পরিবেশে নিম্নতম এনার্জি লেভেলগুলো পূর্ণ হবে, উচ্চ এনার্জি লেভেলগুলো খালি থাকবে।”

• বস (Boson): যেমন ফোটন, যা অনির্দিষ্ট সংখ্যক বস একই কোয়ান্টাম অবস্থায় থাকতে পারে।

• উদাহরণ: একটি ক্যাভিটিতে (চোয়ালা ঘরে) আলো (ফোটন) ভরতে দিন; Bose–Einstein বণ্টন বলবে, “কিছু ফোটন নিম্ন এনার্জি অবস্থায় জমা হতে পারে,” একইভাবে যেমন বোজ-আইনস্টাইন সংঘন (condensation) ঘটতে পারে—যদিও বাস্তবে তা ছায়াচ্ছন্ন সুপারকুলড গ্যাসে দেখা যায়।

পরিসংখ্যানিক মেকানিক্স আবিষ্কারের ধাপসমূহ

1. পরিপাটি থার্মোডাইনামিক্স

   • প্রথমেই তাপগতীয় নিয়ম (থার্মোডাইনামিক্সের প্রথম ও দ্বিতীয় সূত্র) ভালোভাবে বুঝুন।

   • জানুন, তাপমাত্রা তাপগতীয় এনার্জির একটি মাত্রা, আর এনার্জি সংরক্ষণ আইন সর্বদা প্রযোজ্য।

2. মাইক্রোস্টেট সিস্টেম এবং এন্সেম্বল (Ensemble)

   • মাইক্রোস্টেট: একটি নির্দিষ্ট এনার্জি, ভলিউম এবং কণার সংখ্যা ধরে রাখা সিস্টেম।

   • ক্যানোনিক্যাল এন্সেম্বল: স্থির তাপমাত্রা T, ভলিউম V, কণার সংখ্যা N ধরে রাখা।

   • ধারণা: “একই T,V,Nমানের অসংখ্য সিস্টেমের সমষ্টিগত আচরণ” বিবেচনা করে গড় মান বের করা।

3. পার্টিশন ফাংশন Z
   
   

   • ক্যানোনিক্যাল এন্সেমব্লে:

     $$Z(T,V,N)\;=\;\sum_i e^{-E_i/(k_B T)}$$
     
     
     যেখানে Eiহল ‌‌i-তম মাইক্রোস্টেটের এনার্জি, kBবলৎৎস বোল্টসম্যান ধ্রুবক।

   • $\mathrm{Z\; থেকে\; আমরা\; বের\; করতে\; পারি<span\; style="text-align:\; justify;"><br></span>}$

     • গিবস ফ্রি এনার্জি: 
       $F=-k_B T\ln Z$
       
       

     • অভ্যন্তরীণ এনার্জি: 
       $\langle E\rangle = -\partial \ln Z / \partial (1/k_B T)$
       
       

     • চাপ: 
       $P = k_B T\,\partial \ln Z / \partial V$
       
       

4. Maxwell–Boltzmann বণ্টন

   • একটি গ্যাসে একক কণার এনার্জি ε অনুযায়ী জনসংখ্যা:
     $$f(\varepsilon)\propto g(\varepsilon)\,e^{-\varepsilon/(k_B T)}$$
     
     
     যেখানে g(ε)হল ঘনত্ব ফাংশন (density of states)।

   • Discovery: থার্মোডাইনামিক্স + স্ট্যাটিস্টিক্যাল এন্সেম্বল থেকে Z→ তার আয়োজনে একক কণার বণ্টন পান।

কোয়ান্টাম স্ট্যাটিস্টিক্স আবিষ্কারের ধাপসমূহ

1. কোয়ান্টাম অবিচ্ছেদ্যতা (Indistinguishability)

   • ফার্মিয়ন (Fermion) এবং বস (Boson) কণার মধ্যে পার্থক্য:

     • ফার্মিয়নদের ক্ষেত্রে Pauli exclusion principe (একই কোয়ান্টাম অবস্থা একের বেশি ফার্মিয়ন দখল করতে পারে না)

     • বসেরা একই অবস্থা অনবরত নিতে পারে।

2. গ্র্যান্ড ক্যানোনিক্যাল এন্সেম্বল

   • গ্র্যান্ড এন্সেম্বল: Tএবং রাসায়নিক সম্ভাব্যতা μস্থিত, ভলিউম V।

   • গ্র্যান্ড পার্টিশন ফাংশন:

     $$\Xi(T,V,\mu)=\sum_{N=0}^\infty e^{\mu N/(k_B T)}\,Z(T,V,N)$$
     
     

3. Fermi–Dirac বণ্টন (ফার্মিয়নদের জন্য)

   • গড় অভ occupation সংখ্যা:

     $$\langle n_i\rangle = \frac{1}{e^{(\varepsilon_i-\mu)/(k_B T)}+1}$$

   • Discovery: গ্র্যান্ড এন্সেম্বল থেকে Ξ→ অংশীদারি (occupation) গড় বের করা।

4. Bose–Einstein বণ্টন (বসদের জন্য)

   • গড় অভ occupation সংখ্যা:

     $$\langle n_i\rangle = \frac{1}{e^{(\varepsilon_i-\mu)/(k_B T)}-1}$$

5. প্রয়োগ

   • ধরা যাক: ধাতুর ইলেকট্রন (ফার্মিয়ন)—Fermi–Dirac বণ্টন ব্যবহার করে বৈদ্যুতিক পরিবাহীতা বিশ্লেষণ।

   • ধরা যাক: সুপারকুলড বোজ-গ্যাসে Bose–Einstein সংঘন (condensation) → সব কণাই lowest-energy state-এ চলে যায়।

ঐতিহাসিক পটভূমি

পরিসংখ্যানিক পদার্থবিজ্ঞানের ভিত্তি ১৯ শতকের শেষভাগে ম্যাক্সওয়েল, বোল্টজম্যান ও গিবস দ্বারা স্থাপিত হয়। ম্যাক্সওয়েলের গ্যাসের গতি-থিওরি থেকেই এই ধারার সূচনা, এবং বোল্টজম্যান ensemble ধারণা প্রবর্তন করেন। গিবস পরবর্তীতে পরিসংখ্যানিক পদার্থবিজ্ঞান এবং তাপগতিবিদ্যার সমতা প্রতিষ্ঠা করেন। ১৯০৫ সালে আইনস্টাইন ব্রাউনীয় গতি ও photoelectric ঘটনাসহ সংশ্লিষ্ট তাত্ত্বিক উন্নতি করেন। পরে ১৯২৪ সালে সত্যেন্দ্রনাথ বসু ফোটন গ্যাসের জন্য Bose–Einstein পরিসংখ্যান প্রবর্তন করেন। এর পরবর্তী বছরগুলোতে আইনস্টাইন বসুর বণ্টন সূত্রকে পারমাণবিক গ্যাসের জন্য বিস্তৃত করেন। ১৯২৬ সালে এনরিকো ফের্মি ও পল ডির্যাক ফার্মি–ডিরাক পরিসংখ্যান প্রকাশ করেন।

• ১৮৫৯: ম্যাক্সওয়েল গ্যাস অণুর বেগ বণ্টনের সূত্র প্রণয়ন করেন।

• ১৮৭০–৯০: লুডভিগ বোল্টজম্যান তাপগতিবিদ্যাকে মাইক্রোস্টেটের সংখ্যার মাধ্যমে ব্যাখ্যা দেন।

• ১৮৮৪: গিবস পরিসংখ্যানিক পদার্থবিজ্ঞানের নাম প্রবর্তন করেন এবং ensemble ধারণা বিকশিত করেন।

• ১৯০৫: আইনস্টাইন ব্রাউনীয় গতি ও ফোটোইলেকট্রিক প্রভাব প্রণয়ন করেন।

• ১৯২৪: বসু–আইনস্টাইন পরিসংখ্যান ফোটন গ্যাসের জন্য উদ্ভাবিত হয়।

• ১৯২৬: ফের্মি ও ডির্যাক ফের্মি–ডিরাক পরিসংখ্যান প্রতিষ্ঠা করেন।

পরিসংখ্যানিক মেকানিক্সের মৌলিক নীতি

পরিসংখ্যানিক মেকানিক্সের মূল ধারণা হচ্ছে—একটি বৃহৎ সংখ্যার কণা (যেমন গ্যাস অণু) এর প্রতিটি মাইক্রো-অবস্থা (microstate) সমান সম্ভাবনাই হওয়া উচিত যদি সেগুলো একে অপরের সমতুল্য (energetically indistinguishable) হয়। এর কাছ থেকে আমরা নিম্নলিখিত মূল নীতিতে পৌঁছাই:

1. সম সম্ভাবনা (Equal a priori probability): যদি কোনো সিস্টেম নির্দিষ্ট এনার্জি, ভলিউম ও কণার সংখ্যা ধরে রাখে, তাহলে তার সব কাযর্ক্রমযোগ্য মাইক্রোস্টেট সমান সম্ভাবনায় উপস্থিত হতে পারে।

2. এন্সেম্বল পদ্ধতি (Ensemble approach): একক সিস্টেমের পরিবর্তে একই নিয়ামক মান (T, V, N) দেওয়া অসংখ্য সিস্টেমের “গড়” ব্যবহার করে ম্যাক্রোস্কোপিক পরিমাণ (যেমন চাপ, এনার্জি) নির্ণয় করা হয়।

3. পার্টিশন ফাংশন (Partition function):

   $$Z=\sum_i e^{-E_i/(k_B T)}$$
   
   

   এই ফাংশন থেকেই অভ্যন্তরীণ এনার্জি, ফ্রি এনার্জি, চাপ ইত্যাদি ম্যাক্রো পরিমাণ বের করা যায়।

4. Ergodic Hypothesis: পর্যাপ্ত দীর্ঘ সময় পর্যালোচনায় কোনো একক সিস্টেম তার সব মাইক্রোস্টেট পরিদর্শন করবে, তাই সময় গড় (time average) এবং এন্সেম্বল গড় (ensemble average) সমান হবে।

এই নীতিগুলো মিলে Maxwell–Boltzmann বণ্টন, তাপগতিক সমীকরণ ইত্যাদি উদ্ভব করে, যা বহু কণার আচরণকে সহজ ভাবে বর্ণনা করতে সক্ষম করে।

কোয়ান্টাম স্ট্যাটিস্টিক্সের মৌলিক নীতি

কোয়ান্টাম স্তরে কণাগুলো অপরিচ্ছেদ্য (indistinguishable) এবং কোয়ান্টাইজড এনার্জি স্তরে থাকতে বাধ্য—এগুলোকে বিবেচনায় নিয়ে quantum statistics গড়ে ওঠে:

1. অপরিচ্ছেদ্যতা (Indistinguishability): কোয়ান্টাম কণাগুলোকে নাম ধরে আলাদা করা যায় না; কণাসংখ্যা ও এনার্জি বিন্যাসকেই বিবেচনা করা হয়।

2. ফার্মিয়ন বনাম বস (Fermions vs. Bosons):

   • ফার্মিয়ন (Fermion): Pauli exclusion principle অনুযায়ী একই কোয়ান্টাম অবস্থা একের বেশি কণাকে দখল করতে দেয় না। এদের বণ্টন Fermi–Dirac:

     $$\langle n_i\rangle = \frac{1}{e^{(\varepsilon_i-\mu)/(k_B T)}+1}$$

   • বস (Boson): একই অবস্থা অনির্দিষ্ট সংখ্যক বস туда পারে; তাদের বণ্টন Bose–Einstein:

     $$\langle n_i\rangle = \frac{1}{e^{(\varepsilon_i-\mu)/(k_B T)}-1}$$

3. রাসায়নিক সম্ভাব্যতা (Chemical potential, 
   $\mu$

4. কোয়ান্টাম সংঘন (Quantum condensation): যথাযথ শর্তে (নিম্ন তাপমাত্রা, উচ্চ সান্দ্রতা) Boson-রা একত্রে ন্যূনতম এনার্জি অবস্থায় জমা হতে পারে (Bose–Einstein condensation) এবং Fermion-রা Fermi  ঘিরে পূর্ণ বা ফাঁকা লেভেলে সাজেন।

পরিসংখ্যানিক মেকানিক্সের মৌলিক পদার্থবিজ্ঞান

১. মাইক্রোস্টেট ও ম্যাক্রোস্টেট

• মাইক্রোস্টেট: একটি সিস্টেমের প্রতিটি কণার নির্দিষ্ট অবস্থান ও গতি (momentum) মিলিয়ে তৈরি সম্ভাব্য অবস্থা।

• ম্যাক্রোস্টেট: শুধু সার্বিক পরিমাণ (যেমন তাপমাত্রা, চাপ, ভলিউম) দিয়ে বর্ণিত অবস্থা।

২. সম সম্ভাবনা (Equal a priori probability)

• কোনো নির্বিচারে (isolated) সিস্টেম যদি স্থির এনার্জি E, ভলিউম $V$ এবং কণার সংখ্যা Nধরে রাখে, তবে তার সব মাইক্রোস্টেটের সম্ভাবনা সমান।

৩. থার্মোডাইনামিক কনজেকশন

• তাপমাত্রাT↔ গড় গতিশক্তি:
  $$\tfrac{1}{2}m\langle v^2\rangle = \tfrac{3}{2}k_B T$$
  
  

• চাপ  P↔ কণাগুলোর দেয়াল সঙ্গে ধাক্কা:
  PV=NkB​T.  (Ideal gas law)

৪. পার্টিশন ফাংশন 

$Z$

• গণনা:

  $$Z(T,V,N)\;=\;\sum_i e^{-E_i/(k_B T)}$$
  
  

• ব্যবহার:

  • অভ্যন্তরীণ এনার্জি: 
    $\langle E\rangle = -\frac{\partial \ln Z}{\partial (1/k_B T)}$

  • ফ্রি এনার্জি: 
    $F = -k_B T\ln Z$

  • চাপ: 
    $P = k_B T\,\frac{\partial \ln Z}{\partial V}$

৫. চাপ, এনার্জি ও এন্ট্রপি

• এন্ট্রপি S: মাইক্রোস্টেটের সংখ্যা Ωথেকে:=kBlnΩ
  
  

• এই এন্ট্রপি থার্মোডাইনামিক্সের দ্বিতীয় সূত্রকে নিশ্চিত করে: “এন্ট্রোপি সর্বোচ্চ দিকে অগ্রসর হয়”।

কোয়ান্টাম স্ট্যাটিস্টিক্সের মৌলিক পদার্থবিজ্ঞান

১. কোয়ান্টাম অবিচ্ছেদ্যতা (Indistinguishability)

• ফার্মিয়ন ও বস উভয়ই “অপরিচ্ছেদ্য” অর্থাৎ একক কণার স্বাতন্ত্র্য বিবেচ্য নয়; শুধুমাত্র কণার সংখ্যা ও এনার্জি বিন্যাস গুরুত্বপূর্ণ।

২. পাউলি এক্সক্লুশন (Pauli Exclusion Principle)

• ফার্মিয়ন (যেমন ইলেকট্রন): কোনো কোয়ান্টাম অবস্থা দুইটির বেশি কণাকে দখল করতে দেয় না।

• বস (যেমন ফোটন): একই অবস্থা অনির্দিষ্ট সংখ্যক বস থাকতে পারে।

৩. গ্র্যান্ড ক্যানোনিক্যাল এন্সেম্বল

• রাসায়নিক সম্ভাব্যতা μ: সিস্টেমে কণা যোগ বা বিয়োগের এনার্জি খরচকে নির্দেশ করে।

• গ্র্যান্ড পার্টিশন ফাংশন দিয়ে গড় দখল ⟨ni⟩পাওয়া হয়:

  • Fermi–Dirac (ফার্মিয়ন):

    $$\langle n_i\rangle = \frac{1}{e^{(\varepsilon_i - \mu)/(k_B T)} + 1}$$

  • Bose–Einstein (বস):

    $$\langle n_i\rangle = \frac{1}{e^{(\varepsilon_i - \mu)/(k_B T)} - 1}$$

৪. ফার্মি এনার্জি ও ফার্মি তাপমাত্রা

• ফার্মি এনার্জি εF​: T=0এ শেষ পর্যন্ত পূর্ণ থাকা এনার্জি লেভেল।

• উচ্চ Tএ কিছু ফার্মিয়ন εF এর উপরে উত্তলে যায়, যা ধাতুর পরিবাহিতা প্রভাবিত করে।

৫. কোয়ান্টাম প্রকাশ্যতা (Quantum Degeneracy)

• যখন থার্মাল ডি ব্রয়েল তরঙ্গদৈর্ঘ্য λdB∼n−1/3 হয়ে যায়, তখন কোয়ান্টাম প্রভৃতি প্রকাশিত হয়—মিশ্রণে Maxwell–Boltzmann র পরিবর্তে Fermi বা Bose বণ্টন প্রযোজ্য।

৬. বোজ-আইনস্টাইন সংঘন (BEC)

• পর্যাপ্ত শীতল তাপমাত্রায় Boson-রা ground state-এ “সংঘন” হয়ে যায়, ফলে সুপারফ্লুইডিটি, সুপারকন্ডাক্টিভিটি বা নিজস্ব বিকিরণ বৈশিষ্ট্য দেখা দেয়।

মৌলিক ধারণা

পরিসংখ্যানিক পদার্থবিজ্ঞানে মাইক্রোস্টেট হচ্ছে একটি সিস্টেমের সুক্ষ্ম অবস্থা, যেখানে প্রতিটি কণার সঠিক অবস্থান ও গতি নির্ধারিত থাকে। অপরদিকে ম্যাক্রোস্টেট হল সিস্টেমের পরিমাপযোগ্য সামগ্রিক বৈশিষ্ট্যের সংজ্ঞা, যেমন তাপমাত্রা, চাপ, আয়তন ইত্যাদি। একটি নির্দিষ্ট ম্যাক্রোস্টেট একাধিক সম্ভাব্য মাইক্রোস্টেটের সমষ্টি হতে পারে।

পরিসংখ্যানিক সমষ্টি (ensemble) ধারণা Gibbs ও Boltzmann দ্বারা প্রতিষ্ঠিত। মাইক্রোক্যাননিক্যাল সমষ্টি (NVE)-এ সিস্টেমটি বিচ্ছিন্ন থাকে এবং এর মোট শক্তি স্থির থাকে। ক্যাননিক্যাল সমষ্টি (NVT)-এ সিস্টেমটি একটি তাপ সেঁচ (heat bath) এর সঙ্গে যোগাযোগে থাকে, ফলে তাপমাত্রা স্থির থাকে এবং সিস্টেম তাপ বিনিময় করতে পারে। গ্র্যান্ড ক্যাননিক্যাল সমষ্টি (μVT)-এ সিস্টেম তাপ ও কণা উভয়ই বিনিময় করতে পারে, যেখানে রাসায়নিক সম্ভাব্যতা (μ), তাপমাত্রা (T) এবং আয়তন (V) ধ্রুবক ধরা হয়। বোল্টজম্যান এই সমষ্টিগুলোকে বিবেচনা করে সম্ভাবনা গণনা করেন।

পরিসংখ্যানিক ভৌতপদার্থের অসংখ্য মাইক্রোস্টেটের জন্য Partition Function (প্রতিহারের ফাংশন) Z ব্যবহার করা হয়। এটি সব সম্ভাব্য মাইক্রোস্টেটের শক্তি Ei উপর ভিত্তি করে গণনা হয় যেমন

Z=∑ie−Ei/(kBT)

যেখানে kB হলো বোল্টজম্যান ধ্রুবক। এই Z থেকে বিভিন্ন তাপগুণ নির্ধারণ করা যায়।

এন্ট্রপি সংক্রান্ত সূত্রাবলী পার্থক্য অনুযায়ী বিবেচিত হয়। মাইক্রোক্যাননিক্যাল সমষ্টিতে মোট মাইক্রোস্টেট সংখ্যা Ω ধরা হলে বোল্টজম্যান সূত্র অনুযায়ী এন্ট্রপি হয়

S=kBln⁡Ω.S = k_B \ln \Omega.

সাধারণ ক্যাননিক্যাল সমষ্টিতে গিবসের সূত্র অনুসারে এন্ট্রপি নির্ধারিত হয়

S=−kB∑ipiln⁡pi,S = -k_B \sum_i p_i \ln p_i,

যেখানে pi হলো i-তম মাইক্রোস্টেটের সম্ভাবনা। এই দুই সূত্রটি একই উদ্দেশ্য সাধন করে এবং মাইক্রোক্যাননিক্যাল ক্ষেত্রে সহজভাবে S=kB​lnΩ  প্রাপ্তি ঘটে।

বোজ–আইনস্টাইন পরিসংখ্যান

বোজ–আইনস্টাইন পরিসংখ্যান বসু ১৯২৪ সালে উদ্ভাবন করেন এবং পরে আইনস্টাইন এটিকে পরিমার্জন করেন। এই পরিসংখ্যান বোসন (integer-spin কণা) গুলোর জন্য প্রযোজ্য। এর বৈশিষ্ট্য হলো এক অবস্থানে একাধিক বসন থাকতে পারে, কারণ এখানে পাইউলি নিষেধাজ্ঞা প্রযোজ্য নয়। বোজ–আইনস্টাইন কণাগুলি খুব কম তাপমাত্রায় একই ground state-এ “ঘন” হতে পারে, যা Bose–Einstein condensate (BEC) সৃষ্টি করে। উদাহরণস্বরূপ ফোটন গ্যাস এবং হিলিয়াম-৪ সুপারফ্লুইডে এই পরিসংখ্যান প্রয়োগ হয়।

বোস–আইনস্টাইন বিতরণ সূত্র বলে যে i-তম শক্তি স্তরে গড় কণা সংখ্যা

nˉi=gie(εi−μ)/(kBT)−1,\bar{n}_i = \frac{g_i}{e^{(\varepsilon_i - \mu)/(k_B T)} - 1},

যেখানে gi হল ঐ স্তরের অসাম্যতা (degeneracy), εi হল শক্তি, μ রাসায়নিক সম্ভাব্যতা এবং T তাপমাত্রা। লক্ষ্যণীয়, ফোটন গ্যাসে μ =0 হয়। এই বণ্টন ফর্মুলায় ঋণ (+১) না থাকায় একই অবস্থানে অসীমসংখ্যক কণা জমা হতে পারে। এর ফলে লেজার আলো এবং সুপারফ্লুইড হিলিয়ামের মতো ঘটনা বোঝানো যায়।

ফের্মি–ডিরাক পরিসংখ্যান

ফের্মি–ডিরাক পরিসংখ্যান প্রথম প্রকাশিত হয় ১৯২৬ সালে ফার্মি ও ডির্যাকের মাধ্যমে। এটি ফের্মিয়ন (অর্ধ-পূর্ণসংখ্যার স্পিনকণার) জন্য প্রযোজ্য। এই পরিসংখ্যান অনুযায়ী প্রতিটি শক্তি স্তরে সর্বোচ্চ এককণা থাকতে পারে, কারণ পাইউলি নিষেধাজ্ঞা কার্যকর। ফের্মি–ডিরাক বিতরণ অনুযায়ী i-তম স্তরে গড় কণা সংখ্যা হল

nˉi=gie(εi−μ)/(kBT)+1,\bar{n}_i = \frac{g_i}{e^{(\varepsilon_i - \mu)/(k_B T)} + 1},

এখানে প্রতীকগুলোর অর্থ আগের মতই। ঋণচিহ্ন (+১) থাকার ফলে কোনও স্তরে সর্বোচ্চ একটি ফের্মিয়ন অবস্থান নিতে পারে।

ফের্মি–ডিরাক পরিসংখ্যান ধাতুতে ইলেকট্রন গ্যাসের মডেলে ব্যবহৃত হয়। উদাহরণস্বরূপ, ১৯২৭ সালে সোমারফেল্ড মুক্ত ইলেকট্রন মডেলে ইলেকট্রনের আচরণ বোঝাতে এই পরিসংখ্যান প্রয়োগ করেন। এছাড়া হোয়াইট ডয়ার্ফ নক্ষত্রের গণতি এবং ধাতুতে ইলেকট্রন অবস্থা অধ্যয়নে এটিকে গুরুত্ব দেওয়া হয়। সেমিকন্ডাক্টরে ইলেকট্রন-হোল যুগলের কার্যকলাপও ফের্মি–ডিরাক বণ্টন অনুযায়ী বিশ্লেষণ করা হয়, যেখানে রাসায়নিক সম্ভাব্যতাকে ফার্মি স্তর বলে ডাকা হয়।

তুলনামূলক আলোচনা

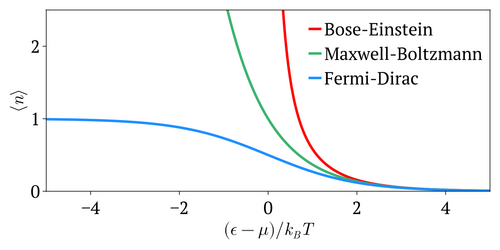
উপরের চিত্রে লাল রেখা Bose–Einstein, নীল রেখা Fermi–Dirac এবং সবুজ রেখা Maxwell–Boltzmann বণ্টনের গড় কণা সংখ্যা প্রদর্শিত হয়েছে। এর থেকে দেখা যায় যে Bose–Einstein পরিসংখ্যানে (বোসন) নিম্ন শক্তিতে গড় কণা সংখ্যা অসীমের কাছাকাছি যেতে পারে (যার ফলে Bose–Einstein ঘনন তৈরি হয়), যেখানে Fermi–Dirac পরিসংখ্যানে (ফের্মিয়ন) গড় কণা সংখ্যা সর্বোচ্চ ১-এ সীমাবদ্ধ থাকে। মূল পার্থক্য হলো বসন-ফের্মিয়নের স্পিন: বসনের পূর্ণসংখ্যক স্পিন, ফের্মিয়নের অর্ধ-পূর্ণসংখ্যক স্পিন। তদুপরি, উচ্চ তাপমাত্রা বা নিম্ন ঘনত্বে উভয়ই Maxwell–Boltzmann (ক্লাসিক্যাল) সীমায় চলে যায়। অর্থাৎ, উভয়ের বণ্টনই ni= e(εi−μ)/(kBT)আকার ধারণ করে।

বাস্তব উদাহরণ

• ব্ল্যাক বডি বিকিরণ: কালদেহ বিকিরণের ফোটন গ্যাস Bose–Einstein পরিসংখ্যান অনুযায়ী বর্ণিত হয় (ফোটন বসন এবং μ=0)।

• ইলেকট্রন গ্যাস (মেটাল): ধাতুতে মুক্ত ইলেকট্রন Fermi–Dirac পরিসংখ্যান মেনে চলে। সোমারফেল্ড মডেলে ধাতুর বৈদ্যুতিক ও উষ্ণতার বৈশিষ্ট্য এই বণ্টনের মাধ্যমে ব্যাখ্যা করা হয়।

• সেমিকন্ডাক্টর: সেমিকন্ডাক্টরের চৌম্বক এবং পরিবাহী ব্যান্ডের ইলেকট্রন-হোল যুগল Fermi–Dirac বণ্টন মেনে চলে। এদের রাসায়নিক সম্ভাব্যতা সাধারণত ফার্মি স্তর হিসেবে ধরা হয়।
  
  

  প্রয়োজনীয় গাণিতিক প্রমাণ

  ১. বোল্টজম্যান এন্ট্রোপি সূত্র

  $$S = k_B \,\ln \Omega$$

  
  

  • কি: এন্ট্রোপি S নির্ণয় করে মাইক্রোস্টেটের সংখ্যা Ω থেকে।

  • মানে: কোনো সিস্টেমে যত বেশি সম্ভাব্য মাইক্রোস্টেট থাকবে (Ω বড় হবে), ততই এন্ট্রোপি বেশি।

  • প্রয়োগ: বিচ্ছিন্ন (isolated) সিস্টেমে, যেখানে শক্তি, আয়তন ও কণার সংখ্যা ধ্রুবক।

  ২. গিবস এন্ট্রোপি সূত্র

  $$S = -k_B \sum_i p_i \,\ln p_i$$

  ​

  • কি: বিভিন্ন মাইক্রোস্টেট iএর সম্ভাবনা pi দিয়ে এন্ট্রোপি গণনা করে।

  • মানে: মাইক্রোস্টেটগুলোর মধ্যে অনিশ্চয়তার পরিমাপ—সম্ভাবনা বণ্টন যত ছড়িয়ে থাকবে, এন্ট্রোপি ততই বেশি।

  • প্রয়োগ: যেকোন ensemble-এ (microcanonical, canonical, grand-canonical) প্রযোজ্য, যেমন তাপ সেঁচের সাথে বিনিময়শীল সিস্টেম।

  ৩. ক্যাননিক্যাল পাটিশন ফাংশন

  $$Z=\sum _i{e}^{-E_i\mathrm{/}(k_{B}T)}$$

  • কি: প্রতিটি মাইক্রোস্টেট iএর শক্তি Ei​ ও তাপমাত্রা T থেকে ensemble-কে স্বাভাবিকীকরণ করে।

  • মানে: Z এর মাধ্যমে সিস্টেমের সমস্ত থার্মোডাইনামিক সুবিধা–অসুবিধা নির্ণয় করা যায়।

  • প্রয়োগ: canonical ensemble (স্থির N,V,T)–এ।

  ৪. বোজ–আইনস্টাইন বণ্টন

  $${\bar{n}}_i=\frac{g_i}{e^{({\epsilon }_i-\mu )\mathrm{/}(k_{B}T)}-\mathrm{1<span\; style="text-align:\; justify;"></span><span\; class="vlist-s"\; style="text-align:\; justify;"></span>}}$$

  • কি: বসন (integer-spin কণা)–এর প্রতিটি শক্তি স্তরে গড় কণা সংখ্যা ni নির্ণয় করে।

  • মানে: “−1” থাকার কারণে একাধিক বসন একই কোয়ান্টাম অবস্থা ভাগাভাগি করে নিতে পারে, ফলে Bose–Einstein ঘনন (condensation) ঘটে।

  • প্রয়োগ: ফোটন গ্যাস, সুপারফ্লুইড Helium-৪, Bose–Einstein condensate ইত্যাদিতে।

  ৫. ফের্মি–ডিরাক বণ্টন

  $$\bar{n}_i = \frac{g_i}{e^{(\varepsilon_i - \mu)/(k_B T)} + 1}$$

  ​​

  • কি: ফের্মিয়ন (half-integer-spin কণা)–এর প্রতিটি শক্তি স্তরে গড় কণা সংখ্যা ni নির্ণয় করে।

  • মানে: “+1” থাকার কারণে পাইউলি নির্বিষ্টাজ্ঞা পালন হয়—এক কোয়ান্টাম অবস্থা সর্বাধিক একটি ফের্মিয়ন পেতে পারে।

  • প্রয়োগ: ধাতুতে মুক্ত ইলেকট্রন, সেমিকন্ডাক্টর, হোয়াইট ডয়ার্ফ নক্ষত্র ইত্যাদিতে।

  ৬. ম্যাক্সওয়েল–বোল্টজম্যান (ক্লাসিক্যাল) সীমা

  $$\bar{n}_i \approx \frac{1}{Z}\,e^{-(\varepsilon_i - \mu)/(k_B T)}$$

  
  

• কি: উচ্চ তাপমাত্রা বা নিম্ন ঘনত্বের ক্ষেত্রে Bose–Einstein এবং Fermi–Dirac উভয়েরই ক্লাসিক্যাল উপসংহার।

• মানে: “±1” কোয়ান্টাম সংশোধন অপ্রাসঙ্গিক হয়ে গেলে কণাগণের বণ্টন সাধারণ এক্সপোনেনশিয়াল ফর্ম নেয়।

• প্রয়োগ: আদর্শ গ্যাস, উচ্চ Tনিম্ন n সীমায় সমস্ত কণা–ধরনে।